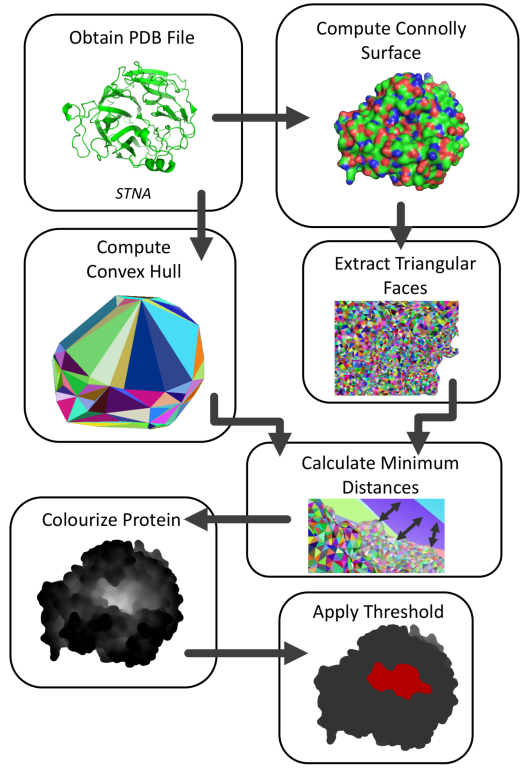
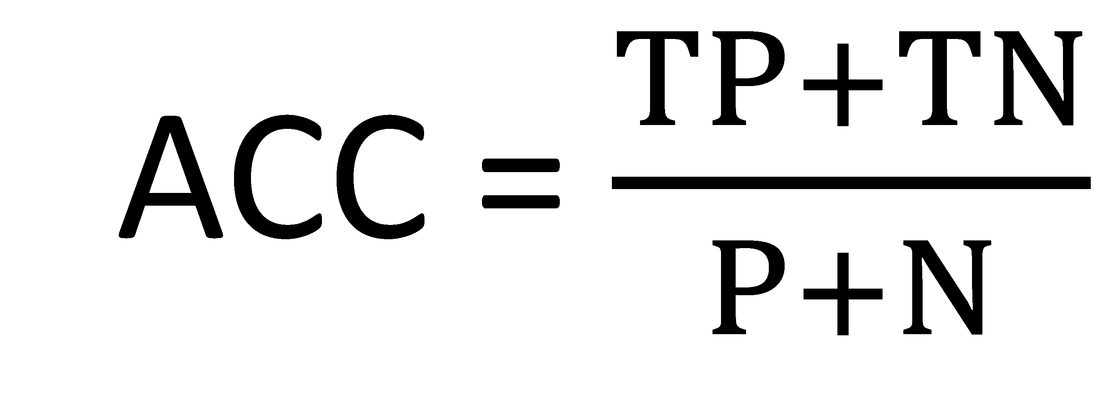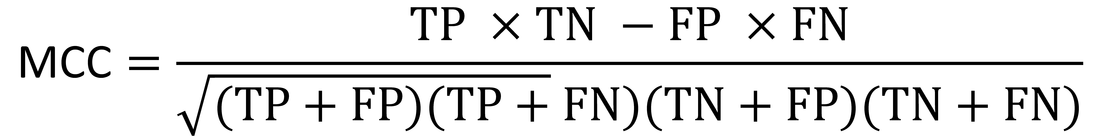The steps within the 3DPocket algorithm are as follows:
- Obtain the protein’s structural file (Crystallographic Information File or CIF) from the RCSB (Research Collaboratory for Structural Bioinformatics) PDB (Protein Data Bank) or elsewhere.
- Use PyMol, a software used to view/manipulate protein structures, to compute the Connolly surface of the protein.
- Export the Connolly surface computed by PyMol to a WRL file written in the Virtual Reality Modeling Language (VRML). Parse the coordinates of all the triangular faces that create the Connolly surface from the WRL file to Python objects (arrays).
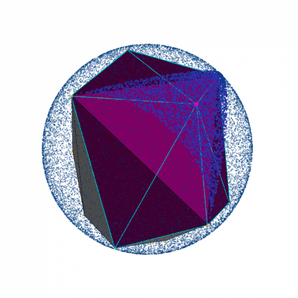
- Use the Quickhull algorithm to compute the 3D convex hull surrounding the protein. Store the coordinates of the triangular faces making up this convex hull.
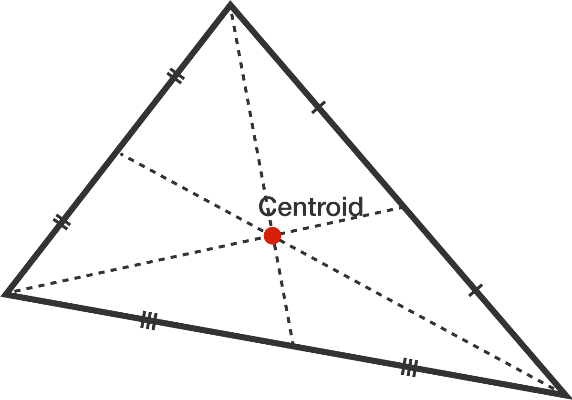
- Calculate the centroid within each triangular face of the Connolly surface.
- Find the coefficients of the scalar equations representing the planes created by each triangular face within the convex hull (3 points define a unique plane).
- Calculate the distance from each centroid to every plane created by the triangular faces within the convex hull (point-to-plane distance).
- Identify the minimum distance from each centroid to the convex hull. Assign these distances as “scores” to each triangular face within the Connolly surface.
- Normalize the set of scores from 0-1 (1 being the largest distance).
- Use the normalized scores to colourize the protein (white representing likely binding sites and black representing unlikely binding sites). This representation of the protein can show a gradient-based view of the binding sites.
- Apply a threshold to distinguish a binding site and a non-binding site. A threshold of scores above 0.4 (when normalized) was primarily used in 3DPocket.
- Obtain the actual, experimentally-determined binding sites from the LIGASITE database. They will be provided as a set of binding residues.
- Convert the set of binding triangular faces identified by applying the threshold to a set of predicted binding residues:
- For every binding triangular face within the Connolly surface representation of the protein, identify all atoms within 1.7 Å.
- Mark these set of atoms as “binding atoms”. Any residue that contains any of these atoms will be considered a “binding residue”.
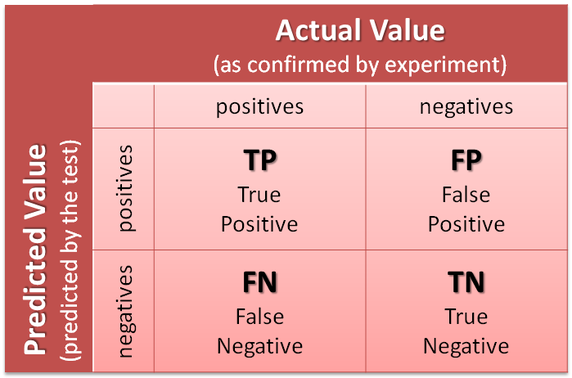
- Create a confusion matrix by comparing the predicted binding residues to the actual binding residues.
- Calculate the accuracy and Matthews correlation coefficient (MCC) values using the confusion matrix (allows for the comparison of 3DPocket to previously created algorithms).
Computing the Convex Hull (Quickhull)
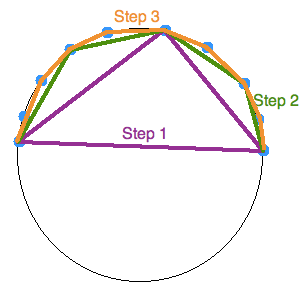
In 2 dimensions, the Quickhull algorithm involves the creation a triangles bounding the interior points recursively. It can be broken down to the following steps:
In 2 dimensions, the Quickhull algorithm involves the creation a triangles bounding the interior points recursively. It can be broken down to the following steps:
- Find the points with minimum and maximum x coordinates —these will always be part of the convex hull.
- Use the line formed by the two points to divide the set in two subsets of points. These subsets will be processed recursively.
- Determine the point, on one side of the line, that is the maximum distance away from the line. The two points found initially, in addition to this one, form a triangle.
- The points contained within the triangle cannot be part of the convex hull and can therefore be ignored in the next steps.
- Repeat the previous two steps on the two lines formed by the triangle (not the initial line).
- Keep on doing so on until no more points are left. Then, the recursion has come to an end and the points selected constitute the convex hull.
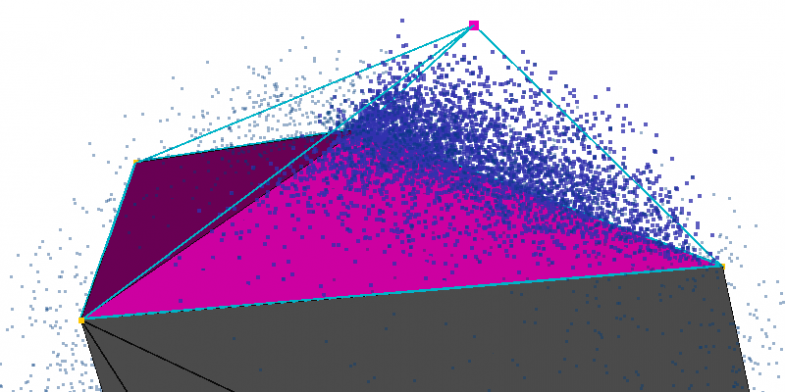
When extending Quickhull to 3 dimensions, tetrahedrons can be used, analogous to triangles in 2 dimensions:
- Initially, the first tetrahedron can be created by choosing 4 points from the 6 extreme points (extreme positive/negative points in the three dimensions—x, y, and z).
- Then, the algorithm can be applied recursively to each of the 4 faces within the tetrahedron (the furthest point from each of these faces can be found to create another tetrahedron).
- This process is continued until no more points are left. Any points contained within the tetrahedrons generated are not part of the convex hull, whereas points selected as vertices of tetrahedrons constitute the convex hull.
Calculating Minimum Distances
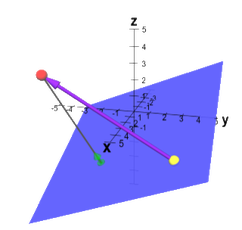
To determine the distance from the Connolly surface to the convex hull, the Connolly surface is first converted into a polyhedron with triangular faces, and the centroid of each face is determined. Then, a plane is constructed from each triangular face of the convex hull, and the point-to-plane distance is calculated between each centroid and every plane (an arbitrary vector connecting the point to the plane can be projected onto the plane’s normal). Next, the minimum distance calculated for each centroid is used to assign a score for the triangular face.
To determine the distance from the Connolly surface to the convex hull, the Connolly surface is first converted into a polyhedron with triangular faces, and the centroid of each face is determined. Then, a plane is constructed from each triangular face of the convex hull, and the point-to-plane distance is calculated between each centroid and every plane (an arbitrary vector connecting the point to the plane can be projected onto the plane’s normal). Next, the minimum distance calculated for each centroid is used to assign a score for the triangular face.
Applying Confusion Matrices
To determine the performance of 3DPocket, a confusion matrix is generated. Such a matrix compares predicted binding sites to those determined experimentally:
To determine the performance of 3DPocket, a confusion matrix is generated. Such a matrix compares predicted binding sites to those determined experimentally:
Then, the accuracy (ACC) and Matthews Correlation Coefficient (MCC) are used to gauge performance against previous algorithms: